4.3.5 Modèle de spectre de mer pleinement développée

La mer est dite pleinement développée quand toutes les vagues sont à l’équilibre, c’est à dire quand le spectre ne dépend que du vent. Il existe de nombreux modèles de spectres pour une mer pleinement développée ([36 , 30, 23, 2, 49]) et une revue de certains des modèles les plus récents, ainsi que l’établissement d’un nouveau modèle de spectre, a été faite par Elfouhaily et al. ([31]). La paramétrisation du spectre des vagues proposée par Elfouhaily et al. a l’avantage d’être applicable aussi bien aux mers pleinement développées qu’aux mers en développement, car elle prend en compte les conditions de fetch⁶ (i.e. des conditions pour lesquelles la mer n’est pas pleinement développée, voir la section 5.1.5).

Le spectre des vagues peut être décomposé schématiquement en quatre domaines de nombre d’onde ([52 ]) ; le domaine du pic spectral (très grandes vagues), le domaine d’équilibre, le domaine des vagues de gravité-capillarité et le domaine des vagues de capillarité (très petite vagues, inférieures au centimètre). Les domaines des plus basses fréquences, pour lesquels k « k_m (domaine du pic spectral et domaine d’équilibre), correspondent à des vagues de gravité. Pour celles-ci, on dérive de (4.32) les vitesses de phase (v_p) et de groupe (v_g) des vagues suivantes

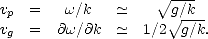(4.45)

La propagation des vagues de gravité (dont la taille est supérieure à plusieurs dizaines de centimètres) est affectée essentiellement par la gravité (voir équations (4.45)), alors que celle des vagues de capillarité (dont la taille est inférieure au centimètre) est fortement affectée par la tension superficielle. Les vagues de capillarité-gravité (de l’ordre de quelques centimètres) sont influencées directement par le vent qui leur transfere de l’énergie qu’elles vont partiellement transmettre aux vagues de plus grande longueur d’onde. Le domaine d’équilibre concerne les vagues dont la taille est éloignée à la fois du pic spectral et de la transition gravité-capillarité (i.e. k = k_m, ce qui correspond à 1.73 cm), et pour lesquelles il est supposé que les termes d’entrée et de dissipation d’énergie s’équilibrent. Phillips ([68]) a établi sur des considérations dimensionnelles que l’expression de 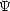(k,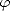₀) dans le domaine d’équilibre était proportionnelle à k^-4 et indépendante du vent. Depuis, Philipps ([69]) a redéfini cette dépendance comme étant une limite majorant l’énergie des vagues (i.e. une saturation) au delà de laquelle les vagues déferlent. En 1985, Philipps a réévalué la dépendence du spectre à l’équilibre comme étant proportionnelle à u_*gk^-3.5, soit, pour le spectre en pulsation, proportionnel u_* g^-4 , où u_* est la vitesse de friction du vent (voir la section 4.3.7) et g est l’accélération de la pesanteur. De nombreux modèles de spectre ([30, 23, 2, 31]) adoptent donc la forme suivante

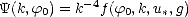(4.46)

où une fonction f rend compte de la différence d’énergie du spectre à un k donné par rapport à un spectre saturé variant en k^-4, différence due au fait que les vagues déferlent à une hauteur plus faible que la hauteur de saturation.

Dans mes simulations d’émissivité, j’ai utilisé principalement le modèle de spectre de Durden et Vesecky ([30 ], appelé DV par la suite). Une compraison de ce modèle de spectre avec le modèle proposé par Elfouhaily et al. ([31], appelé ELF par la suite) ainsi que de leur influence sur Tbmer est exposée dans la section 5.1.3. Le modèle DV est applicable à une mer pleinement développée, c’est à dire à une mer qui est en équilibre avec le vent local et dont, par conséquent, l’énergie des vagues ne dépend que du seul paramètre U, contrairement aux vagues d’une mer en développement dont l’énergie dépend aussi de leur âge (voir la section 5.1.5). En pratique, le spectre est exprimé en fonction du module du vent U pour la partie basses fréquences et de la vitesse de friction u_* pour la partie hautes fréquences. Ces deux paramètres sont reliés par une loi donnée dans la section 4.3.7, si bien que l’on peut déterminer le spectre des vagues à partir de la seule connaissance soit de U, soit de u_*. La loi reliant U et u_* fait intervenir la stabilité de l’atmosphère qui dépend de 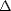T, définie par

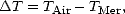(4.47)

où T_Air est la température de l’air à une hauteur de référence et T_Mer = SST. En toute rigueur, il est donc nécessaire de connaître 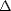T pour déterminer le spectre des vagues. En pratique, je négligerai l’influence de 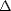T (dont l’ordre de grandeur est discuté dans la section 4.3.7) dans les études exposées dans cette thèse parce que, d’une part, cette influence est relativement faible et parce que, d’autre part, SMOS ne fera pas de mesures de T_Air et que je n’ai pas étudié la possiblité d’en obtenir une estimation par des modèles météorologiques. La loi utilisé pour relier u_* et U permet aussi de le profil vertical du vent, donc passer d’un vent à une altitude donnée à une autre (ce qui va être très utile par la suite, car les modèles de spectres sont fonction de valeurs de vent à des altitudes diverses).

Le spectre de puissance omnidirectionnel, d’après le modèle DV ([30]), est donné par

(4.48)

où k_j = 2, k_c = g/U_19.5 avec g = 9.81 m.s^-2, l’accéleration de la pesanteur, et U_19.5, le module du vent à une altitude de 19.5 m (voir la section 4.3.7 pour calculer le vent à 19.5 m à partir du vent à une autre altitude), g_* = g + 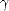k² avec 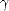= 7.25 × 10^-5m³.s^-2, le rapport entre la tension superficielle et la densité de l’eau. Les constantes a₀ = 0.004 et 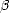= 0.74 sont issues du modèle de spectre de Pierson et Moskowitz ([72 ]) qui a été ajusté sur des mesures d’état de mer ([63]) et b₀ = a₀ exp(1.85 × 10^-1k_c.²) est calculé pour assurer la continuité du spectre en k = 2. Les constantes a = 0.225 et b = 1.25 ont été ajustées par régression sur des données diffusiométriques RADSCAT à 13.9 GHz [30]. Je montrerai dans la section 4.3.8 que la paramétrisation donnée en (4.48) pose problème pour les vents faibles.

Je suppose ici que la ruguosité de surface résulte de l’effet du vent local (i.e. qu’on est en présence d’une mer du vent) ; les vagues sont par conséquent symétriques par rapport à la direction du vent. On utilise donc une fonction d’étalement angulaire symétrique par rapport à la direction du vent, choisie sous la forme

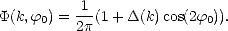(4.49)

La fonction d’étalement angulaire module l’amplitude du spectre omnidirectionnel S(k) en fonction de l’orientation des vagues relativement à la direction du vent (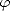₀). La deuxième harmonique (i.e. le terme en cos (2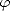₀)) permet de rendre compte de l’asymétrie upwind/crosswind (i.e. entre les directions face au vent/transverse au vent). On peut alors réécrire le calcul des variances des pentes (4.43), (4.44) pour le cas où la fonction d’étalement est de la forme générale (4.49) comme

Dans le modèle de Durden et Vesecky, on a

(4.52)

où s = 1.5 × 10^-4 m²,

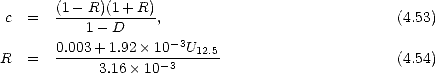
et

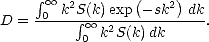(4.55)

Le paramètre c, et donc R et D, ont été définis pour reproduire le rapport entre _u² et _c² observé par Cox et Munk ([14]). Cox et Munk ont estimé la variance des pentes à partir de photographies de l’image du Soleil à la surface de la mer. Les variances des pentes mesurées par Cox et Munk sont reliées au vent par les relations empiriques suivante

où U_12.5 est le module du vent à une hauteur de 12.5 m. Le modèle de spectre de Durden et Vesecky (modèle DV) reproduit 95% de la variance des pentes mesurée par Cox et Munk à U₁₀ 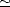10 m.s^-1 ([102]). La figure 4.7 illustre la variance des pentes en fonction du vent déduite du modèle de spectre DV et des lois de Cox et Munk (CM). La variance des pentes du modèle de spectre DV est toujours en très bon accord avec les variances CM. La variance des pentes dans la direction du vent augmente plus rapidement avec le vent que celle dans la direction transverse. Bien que plusieurs modèles de spectres soient construits pour reproduire les variance CM ([30, 31]), des études ont montré que les variances mesurées par Cox et Munk pourraient être sous-estimées ([23, 2, 96]) d’un facteur 1.7 à plus de deux, parceque la variance des pentes mesurée ne correspondrait pas à celle intégrée sur tout le spectre ([30 ]). En conséquence, l’énergie des spectres ajustés sur les variances CM serait sous-estimée. Dans ce contexte, Yueh a proposé de multiplier le modèle DV par un facteur deux ([102 ]). De plus, une fois cette modification du spectre effectuée, les températures de brillance simulées par son modèle s’ajustent mieux avec des données radiométriques à 19.35 GHz et 37 GHz ([102 ]). Lorsque j’utiliserai le modèle de Durden et Vesecky dont l’amplitude est multipliée par un facteur deux, je l’appelerai DV2 (par opposition à DV qui concerne le spectre original).

FIG. 4.7: Variances des pentes mesurées par Cox et Munk ([14]) et calculées à partir du modèle de spectre de Durden et Vesecky ([30]) sur toutes les échelles.

Les modèles de spectre ont une variation proche de k^-4 dans le domaine d’équilibre. Pour supprimer cette variation, on utilise fréquemment le spectre de courbure (ou de saturation) défini comme

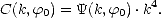(4.58)

On peut décomposer le spectre sous la forme d’une série de Fourier tronquée à l’ordre deux (voir l’annexe H) pour séparer la composante omnidirectionnelle de la variation angulaire azimutale. On a alors

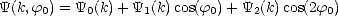(4.59)

où

et donc, d’après (4.26) et (4.49),

Le rapport entre l’amplitude de la variation azimutale du spectre et le spectre moyenné sur toutes les directions est donné par 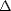(k), défini en (4.49).

On décompose de même le spectre de courbure comme

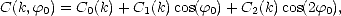(4.67)

où

On utilise aussi le spectre de courbure à une dimension (1D) B(k) = S(k) ^. k³ et le spectre de puissance 1D S(k) reliés aux définitions précédentes par