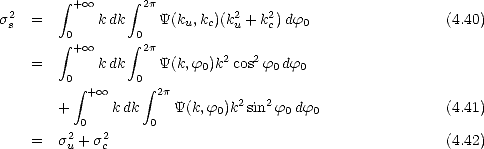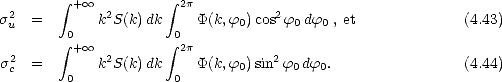Le vent 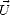 à la surface de la mer va interagir avec elle,
si bien que l’atmosphère et l’océan vont se tranférer mutuellement de l’énergie à travers la
dynamique des vagues de surface. Les vents que rencontrera SMOS à la surface du globe
sont illustrés par des cartes et des histogrammes dans la section 4.6.2 déduits des mesures
sur un jour et à 25 km de résolution du diffusiomètre QSCAT. Le module du vent à une
hauteur de dix mètres au dessus de la surface de l’océan (U10) est en moyenne sur tout le globe
d’environ 8 m.s-1 et l’écart type du module du vent est de 3.5 m.s-1 (d’après les mesures
QSCAT).
à la surface de la mer va interagir avec elle,
si bien que l’atmosphère et l’océan vont se tranférer mutuellement de l’énergie à travers la
dynamique des vagues de surface. Les vents que rencontrera SMOS à la surface du globe
sont illustrés par des cartes et des histogrammes dans la section 4.6.2 déduits des mesures
sur un jour et à 25 km de résolution du diffusiomètre QSCAT. Le module du vent à une
hauteur de dix mètres au dessus de la surface de l’océan (U10) est en moyenne sur tout le globe
d’environ 8 m.s-1 et l’écart type du module du vent est de 3.5 m.s-1 (d’après les mesures
QSCAT).
L’action du vent est dans un premier temps de créer des vagues de petite longueur d’onde auquelles il va
transférer de l’énergie. Ces petites vagues (de l’ordre de quelques centimètres), qui se forment
rapidement sous l’action du vent et qui sont très vite saturées en énergie, vont ensuite former
des vagues de plus grande longueur d’onde par interactions entre vagues tant que le vent
fournira de l’énergie. Ainsi, au cours du temps, une partie de l’énergie fournie par le vent
aux petites vagues est transférée à des vagues de longueur d’onde de plus en plus grande
et une autre partie est dissipée par viscosité ou turbulence. Le développement des grandes
vagues finira par atteindre une limite en longueur d’onde 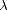 p au delà de laquelle la vitesse de
phase de la vague est tellement rapide que le vent ne lui apporte plus d’énergie. Le spectre de
puissance va donc rapidement décroître au delà de
p au delà de laquelle la vitesse de
phase de la vague est tellement rapide que le vent ne lui apporte plus d’énergie. Le spectre de
puissance va donc rapidement décroître au delà de 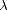 p (ou en deça de kp = 2
p (ou en deça de kp = 2 /
/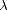 p), ce qui va
aboutir à la présence d’un pic d’amplitude pour le spectre en
p), ce qui va
aboutir à la présence d’un pic d’amplitude pour le spectre en 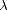 =
= 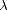 p (ou k = kp). Les vagues
résultant de l’action du vent local et récent constituent la mer du vent, par opposition au
vagues de la houle qui ont voyagé sur une longue distance depuis le lieu de génération par le
vent.
p (ou k = kp). Les vagues
résultant de l’action du vent local et récent constituent la mer du vent, par opposition au
vagues de la houle qui ont voyagé sur une longue distance depuis le lieu de génération par le
vent.
Lorsque, pour des vagues ayant une longueur d’onde donnée, les termes d’entrée d’énergie et de
dissipation se compensent, ces vagues sont à l’équilibre. Pour qu’une mer soit à l’équilibre, il faut que le
vent soit constant sur une durée et une distance suffisamment grands pour que toutes les longueurs d’onde
du spectre soient à l’équilibre. Les vagues de quelques dizaines de mètres peuvent mettre plusieurs
dizaines d’heures pour atteindre l’équilibre ([46]) et nécessiter que le vent souffle sur une distance de
plusieurs dizaines de kilomètres de façon stationnaire ce qui fait qu’une mer n’est jamais rigoureusement à
l’équilibre.
Le spectre de la mer du vent a des propriétés de symétrie par rapport à la direction (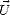 ) du vent qui a
donné naissance aux vagues ; je vais donc utiliser la forme polaire du spectre de puissance donné en (4.19)
qui va me permettre de séparer la composante moyenne du spectre sur toutes les directions (spectre
omnidirectionnel) de la variation azimutale. Le vecteur d’onde
) du vent qui a
donné naissance aux vagues ; je vais donc utiliser la forme polaire du spectre de puissance donné en (4.19)
qui va me permettre de séparer la composante moyenne du spectre sur toutes les directions (spectre
omnidirectionnel) de la variation azimutale. Le vecteur d’onde 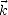 a une norme (i.e. le nombre d’onde) k et
fait un angle
a une norme (i.e. le nombre d’onde) k et
fait un angle 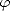 0 avec le vecteur vent (
0 avec le vecteur vent (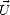 ) dans le plan de référence. On décompose alors
) dans le plan de référence. On décompose alors 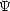 sous la forme
polaire suivante
sous la forme
polaire suivante
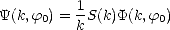 | (4.26) |
où S(k) est la composante omnidirectionnelle du spectre de puissance, et 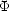 (k,
(k,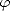 0) est la fonction
d’étalement angulaire, normalisée de sorte que
0) est la fonction
d’étalement angulaire, normalisée de sorte que
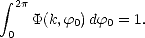 | (4.27) |
On a ainsi
et
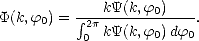 | (4.30) |
C’est le spectre en fréquences spatiales k = 2 /xi qui est utilisé pour les calculs de diffusion des ondes
électromagnétiques à la surface de l’océan, mais c’est souvent le spectre en fréquences temporelles
/xi qui est utilisé pour les calculs de diffusion des ondes
électromagnétiques à la surface de l’océan, mais c’est souvent le spectre en fréquences temporelles  = 1/t
qui est mesuré (voir la section 7.1.2.1 avec les mesures du spectre des grandes vagues par la
bouée houle par exemple). On relie ces deux spectres dans le domaine des grandes vagues par
([31 , 52 ])
= 1/t
qui est mesuré (voir la section 7.1.2.1 avec les mesures du spectre des grandes vagues par la
bouée houle par exemple). On relie ces deux spectres dans le domaine des grandes vagues par
([31 , 52 ])
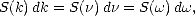 | (4.31) |
avec  = 2
= 2
 , la pulsation, et avec la relation de dispersion suivante
, la pulsation, et avec la relation de dispersion suivante
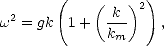 | (4.32) |
où km = 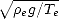 avec
avec 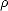 e la densité de l’eau de mer, g l’accélération de la pesanteur et Te la tension
superficielle (km est de l’ordre de 360 rad.m-1 pour g = 9.81 m.s-2, Te = 0.078 N.m-1 et
e la densité de l’eau de mer, g l’accélération de la pesanteur et Te la tension
superficielle (km est de l’ordre de 360 rad.m-1 pour g = 9.81 m.s-2, Te = 0.078 N.m-1 et 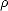 e = 1025
kg.m3 qui sont des valeurs typiques de l’eau de mer). Une discussion sur le passage du spectre
temporel au spectre spatial pour les hautes fréquences (i.e. les petites vagues) est donnée dans
[52 ].
e = 1025
kg.m3 qui sont des valeurs typiques de l’eau de mer). Une discussion sur le passage du spectre
temporel au spectre spatial pour les hautes fréquences (i.e. les petites vagues) est donnée dans
[52 ].
On déduit de (4.21) et de (4.22) respectivement les variances des hauteurs et des pentes de la mer du
vent en coordonnées polaires
En introduisant (4.26) dans (4.33), on obtient la variance des hauteurs suivante
d’où l’on déduit, d’après la normalisation (4.27), que
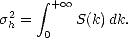 | (4.37) |
De même, en introduisant (4.26) dans (4.34) on obtient la variance des pentes
Les pentes sont a priori anisotropes, car il n’y a pas de raison pour qu’elles soient identiques le long
du vecteur 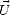 et dans des directions différentes, en particulier dans la direction transverse à
et dans des directions différentes, en particulier dans la direction transverse à 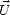 . De plus, on
verra que les pentes des petites vagues sont différentes selon qu’elle sont sur le côté face-au-vent ou sur le
côté sous-le-vent d’une grande vague (phénomène de modulation hydrodynamique). La modulation
hydrodynamique ne peut être restituée par le spectre défini en (4.19) ; elle sera prise en compte par un
modèle empirique (voir la section 4.3.6).
. De plus, on
verra que les pentes des petites vagues sont différentes selon qu’elle sont sur le côté face-au-vent ou sur le
côté sous-le-vent d’une grande vague (phénomène de modulation hydrodynamique). La modulation
hydrodynamique ne peut être restituée par le spectre défini en (4.19) ; elle sera prise en compte par un
modèle empirique (voir la section 4.3.6).
Je vais déterminer l’expression de la variance des pentes  u2 et
u2 et  c2 respectivement dans la direction
du vent (direction face au vent
c2 respectivement dans la direction
du vent (direction face au vent 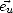 , pour upwind) et le long de la direction transverse au vent (direction
vent de travers
, pour upwind) et le long de la direction transverse au vent (direction
vent de travers 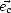 , pour crosswind). On écrit alors
, pour crosswind). On écrit alors 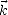 = ku
= ku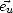 + kc
+ kc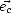 où ku = k cos
où ku = k cos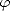 0 et kc = k sin
0 et kc = k sin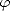 0. On
déduit ensuite de (4.34)
0. On
déduit ensuite de (4.34)
d’où l’on dérive les expressions suivantes
Dans les sections qui suivent, je séparerai le spectre en différents domaines. Il y a tout d’abord, comme
on l’a vu au début de cette section, une séparation liée à la physique des vagues en différents
domaines de longueur d’onde, dans lesquels les vagues ne sont pas générées et entretenues par
les mêmes phénomènes physiques (gravité, capillarité, ... voir la section 4.3.5). Mais il y a
aussi une séparation liée à l’interaction des ondes EM avec les vagues. En effet, la manière
dont cette interaction va se faire dépend de la taille des vagues par rapport à la longueur
d’onde de l’instrument (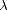 0). On distinguera donc les vagues dont la taille est supérieure à
0). On distinguera donc les vagues dont la taille est supérieure à
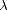 0 , ce que j’appellerai les grandes échelles (GE) et les vagues dont la taille est de l’ordre
de et inférieure à
0 , ce que j’appellerai les grandes échelles (GE) et les vagues dont la taille est de l’ordre
de et inférieure à 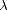 0, ce que j’appellerai les petites échelles (PE) (voir les sections 4.3.6 et
4.4).
0, ce que j’appellerai les petites échelles (PE) (voir les sections 4.3.6 et
4.4).
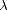 p au delà de laquelle la vitesse de
phase de la vague est tellement rapide que le vent ne lui apporte plus d’énergie. Le spectre de
puissance va donc rapidement décroître au delà de
p au delà de laquelle la vitesse de
phase de la vague est tellement rapide que le vent ne lui apporte plus d’énergie. Le spectre de
puissance va donc rapidement décroître au delà de 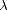 p (ou en deça de kp = 2
p (ou en deça de kp = 2 /
/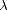 p), ce qui va
aboutir à la présence d’un pic d’amplitude pour le spectre en
p), ce qui va
aboutir à la présence d’un pic d’amplitude pour le spectre en 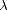 =
= 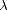 p (ou k = kp). Les vagues
résultant de l’action du vent local et récent constituent la mer du vent, par opposition au
vagues de la houle qui ont voyagé sur une longue distance depuis le lieu de génération par le
vent.
p (ou k = kp). Les vagues
résultant de l’action du vent local et récent constituent la mer du vent, par opposition au
vagues de la houle qui ont voyagé sur une longue distance depuis le lieu de génération par le
vent.
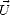 à la surface de la mer va interagir avec elle,
si bien que l’atmosphère et l’océan vont se tranférer mutuellement de l’énergie à travers la
dynamique des vagues de surface. Les vents que rencontrera SMOS à la surface du globe
sont illustrés par des cartes et des histogrammes dans la section 4.6.2 déduits des mesures
sur un jour et à 25 km de résolution du diffusiomètre QSCAT. Le module du vent à une
hauteur de dix mètres au dessus de la surface de l’océan (
à la surface de la mer va interagir avec elle,
si bien que l’atmosphère et l’océan vont se tranférer mutuellement de l’énergie à travers la
dynamique des vagues de surface. Les vents que rencontrera SMOS à la surface du globe
sont illustrés par des cartes et des histogrammes dans la section 4.6.2 déduits des mesures
sur un jour et à 25 km de résolution du diffusiomètre QSCAT. Le module du vent à une
hauteur de dix mètres au dessus de la surface de l’océan (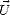 ) du vent qui a
donné naissance aux vagues
) du vent qui a
donné naissance aux vagues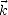 a une norme (i.e. le nombre d’onde)
a une norme (i.e. le nombre d’onde) 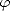
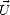 ) dans le plan de référence. On décompose alors
) dans le plan de référence. On décompose alors 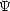 sous la forme
polaire suivante
sous la forme
polaire suivante
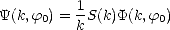
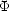 (
(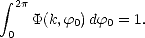
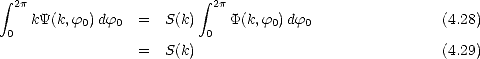
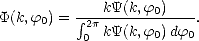

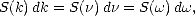

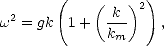
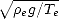 avec
avec 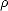
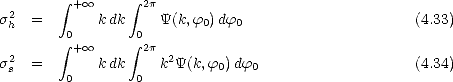
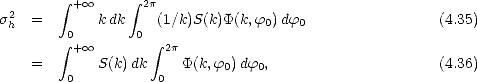
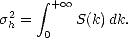
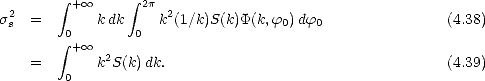
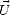 et dans des directions différentes, en particulier dans la direction transverse à
et dans des directions différentes, en particulier dans la direction transverse à 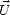 . De plus, on
verra que les pentes des petites vagues sont différentes selon qu’elle sont sur le côté face-au-vent ou sur le
côté sous-le-vent d’une grande vague (phénomène de modulation hydrodynamique). La modulation
hydrodynamique ne peut être restituée par le spectre défini en (
. De plus, on
verra que les pentes des petites vagues sont différentes selon qu’elle sont sur le côté face-au-vent ou sur le
côté sous-le-vent d’une grande vague (phénomène de modulation hydrodynamique). La modulation
hydrodynamique ne peut être restituée par le spectre défini en (
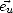 , pour
, pour 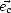 , pour
, pour 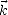 =
= 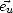 +
+ 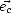 où
où