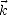 , que
l’on appelle le plan de polarisation Pp, et qu’ils sont orthogonaux entre eux (voir la figure
4.1).
, que
l’on appelle le plan de polarisation Pp, et qu’ils sont orthogonaux entre eux (voir la figure
4.1).
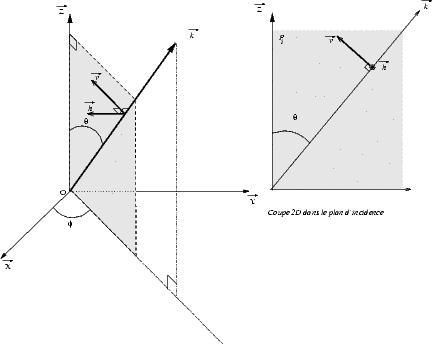
On a vu dans la section 2.1.1 et dans l’annexe A que les champs électrique et magnétique
d’une onde plane sont contenus dans le plan orthogonal à la direction de propagation 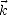 , que
l’on appelle le plan de polarisation Pp, et qu’ils sont orthogonaux entre eux (voir la figure
4.1).
, que
l’on appelle le plan de polarisation Pp, et qu’ils sont orthogonaux entre eux (voir la figure
4.1).
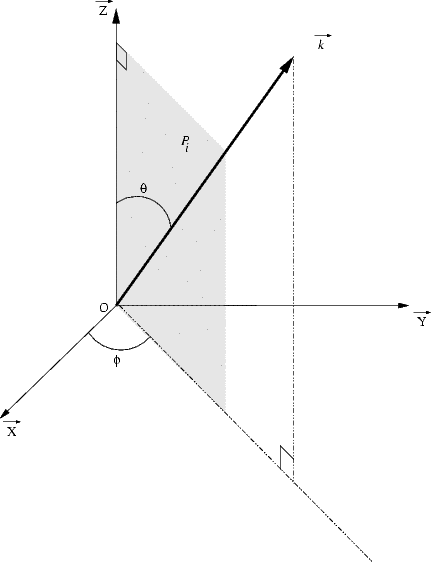
Il existe cependant une infinité de directions dans le plan de polarisation et l’on va définir deux
d’entres elles comme directions de référence. On définit tout d’abord le plan d’incidence Pi comme étant
le plan formé par la normale à la surface de la Terre 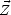 et par la direction de propagation de l’onde
et par la direction de propagation de l’onde 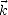 (voir
figure 4.2).
(voir
figure 4.2).
|
|
On définit la direction verticale 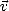 , aussi appelée parallèle, comme appartenant à
Pi et Pp , et la direction horizontale
, aussi appelée parallèle, comme appartenant à
Pi et Pp , et la direction horizontale 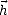 , aussi appelée perpendiculaire, comme étant
orthogonale à Pi et appartenant à Pp. L’onde EM est dite polarisée verticalement (V-pol) ou
horizontalement (H-pol) selon que le champ
, aussi appelée perpendiculaire, comme étant
orthogonale à Pi et appartenant à Pp. L’onde EM est dite polarisée verticalement (V-pol) ou
horizontalement (H-pol) selon que le champ 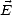 soit respectivement le long de
soit respectivement le long de 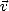 ou de
ou de
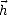 1. Les
polarisations horizontale et verticale sont illustrées sur la figure 4.3. On peut ainsi décomposer les
vecteurs
1. Les
polarisations horizontale et verticale sont illustrées sur la figure 4.3. On peut ainsi décomposer les
vecteurs 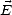 et
et 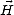 en composantes polarisées verticalement et horizontalement, ce qui conduit
à
en composantes polarisées verticalement et horizontalement, ce qui conduit
à
où Ev et Hv sont respectivement les amplitudes des champs 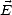 et
et 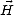 en V-pol et où Eh et Hh sont les
amplitudes de ces mêmes champs en H-pol.
en V-pol et où Eh et Hh sont les
amplitudes de ces mêmes champs en H-pol.
|
|
Lorsque l’on se place dans un plan de polarisation donné (i.e. à z = constante si l’onde se déplace le
long de 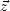 =
= 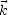 / ||
/ ||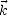 ||), les extrémités des vecteurs
||), les extrémités des vecteurs 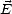 et
et 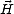 décrivent au cours du temps des courbes dans le
plan de polarisation. Ces courbes vont caractériser la polarisation de l’onde EM. Lorsque
les extrémités des vecteurs décrivent une droite, c’est à dire lorsque que le champ varie en
amplitude mais est toujours orienté dans la même direction, l’onde est polarisée linéairement. Les
polarisations verticale et horizontale sont des exemples de polarisation linéaire. Lorsque les
extrémités des vecteurs décrivent un cercle ou une ellipse, l’onde est polarisée respectivement
circulairement ou elliptiquement ; les polarisations circulaire et elliptique peuvent toujours être
décomposées comme la superposition de deux polarisations linéaires othogonales entre elles
([90 ]). Les polarisations linéaires, circulaires et elliptiques caractérisent des ondes totalement
polarisées.
décrivent au cours du temps des courbes dans le
plan de polarisation. Ces courbes vont caractériser la polarisation de l’onde EM. Lorsque
les extrémités des vecteurs décrivent une droite, c’est à dire lorsque que le champ varie en
amplitude mais est toujours orienté dans la même direction, l’onde est polarisée linéairement. Les
polarisations verticale et horizontale sont des exemples de polarisation linéaire. Lorsque les
extrémités des vecteurs décrivent un cercle ou une ellipse, l’onde est polarisée respectivement
circulairement ou elliptiquement ; les polarisations circulaire et elliptique peuvent toujours être
décomposées comme la superposition de deux polarisations linéaires othogonales entre elles
([90 ]). Les polarisations linéaires, circulaires et elliptiques caractérisent des ondes totalement
polarisées.
Lors de processus radiatifs naturels, comme l’émission thermique par exemple, les ondes EM émises ne sont pas totalement polarisées et ne sont donc pas décomposables comme la somme d’ondes polarisées linéairement, circulairement et elliptiquement. Pour décrire la polarisation d’une onde EM totalement, partiellement ou non polarisée, on utilise les quatres paramètres de Stokes ([48, 11]) qui définissent le vecteur de Stokes. Les paramètres de Stokes décrivent la puissance totale transportée par l’onde et la répartition de cette puissance parmi les composantes de l’onde polarisées linéairement et circulairement. Le vecteur de Stokes s’écrit sous la forme
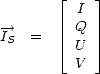
où le premier paramètre de Stokes, I, représente la puissance totale transportée par l’onde, c’est à dire la puissance transportée par les composantes polarisées et non polarisées. Le second paramètre de Stokes, Q, est définit comme la différence de puissance entre deux polarisations linéaires, orientées le long de deux directions de référence ; ces polarisations linéaires de référence sont V- et H-pol, c’est à dire que Q est la différence de puissance entre les polarisations verticale et horizontale. U est la différence de puissance entre les polarisations linéaires orientées à +45o et -45o de la polarisation verticale. V est la différence de puissance entre les polarisations circulaires gauche et droite2 . Les deux premiers paramètres de Stokes (i.e. I et Q) donnent la décomposition de la puissance sur les V- et H-pol, et les deux derniers paramètres (i.e. U et V ) donnent la corrélation des champs en V- et H-pol.
On définit les paramètres de Stokes normalisés à la puissance totale I pour obtenir la répartition relative de la puissance sur les différentes polarisations. Les quatres paramètres de Stokes normalisés sont défini par i = I/I = 1,q = Q/I,u = U/I et v = V/I. On décompose alors n’importe quelle polarisation sur une base de quatres vecteurs de Stokes normalisés choisis parmi:
| (1, 1, 0, 0) | onde polarisée linéairement en V-pol, |
| (1,-1,0,0) | onde polarisée linéairement en H-pol, |
| (1,0,1,0) | onde polarisée à 45o de la polarisation verticale, |
| (1, 1, -1, 0) | onde polarisée à -45o de la polarisation verticale, |
| (1, 0, 0, 1) | onde polarisée circulairement à gauche, |
| (1, 1, 0, -1) | onde polarisée circulairement à droite. |
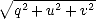 < 1 (ou
< 1 (ou 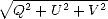 < I), l’onde est partiellement polarisée. Si
i = 1, q = u = v = 0, il n’y a pas de corrélation entre les composantes verticales et horizontales des
champs et la puissance moyenne de l’onde est identique dans toutes polarisations. Une telle onde est
non-polarisée (cas de la lumière naturelle). Enfin, si
< I), l’onde est partiellement polarisée. Si
i = 1, q = u = v = 0, il n’y a pas de corrélation entre les composantes verticales et horizontales des
champs et la puissance moyenne de l’onde est identique dans toutes polarisations. Une telle onde est
non-polarisée (cas de la lumière naturelle). Enfin, si 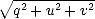 = 1, l’onde est totalement
polarisée.
= 1, l’onde est totalement
polarisée.
Pour relier I,Q,U et V au champ EM, il faut déterminer la puissance transportée par une onde EM.
La puissance transportée par une onde EM à travers une surface est déterminée par le flux du vecteur de
Poynting à travers cette surface ([16]). Le vecteur de Poynting instantanné en notation complexe 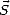 ci est
donné par
ci est
donné par
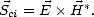 | (4.3) |
On déduit de (4.3) le vecteur de Poynting moyen 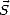 cm sur une période de l’onde EM ([48]), qui
caractérise le flux de la puissance moyenne transportée par l’onde
cm sur une période de l’onde EM ([48]), qui
caractérise le flux de la puissance moyenne transportée par l’onde
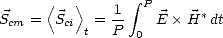 | (4.4) |
où P est la période de l’onde et  t désigne une moyenne temporelle. Pour une onde plane
monochromatique dont les champs électrique et magnétique sont définis par (A.8) et (A.12) (i.e. une onde
qui varie sinusoïdalement avec le temps), on obtient ([78, 90, 89])
t désigne une moyenne temporelle. Pour une onde plane
monochromatique dont les champs électrique et magnétique sont définis par (A.8) et (A.12) (i.e. une onde
qui varie sinusoïdalement avec le temps), on obtient ([78, 90, 89])
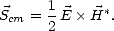 | (4.5) |
Comme le vecteur d’onde 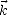 est orthogonal à
est orthogonal à 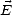 et
et 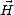 , on en déduit que la puissance transportée est
le long du vecteur d’onde. De plus,
, on en déduit que la puissance transportée est
le long du vecteur d’onde. De plus, 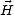 est orthogonal à
est orthogonal à 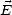 et son amplitude |
et son amplitude |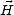 | est égale à
1/
| est égale à
1/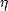 |
|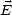 | (voir l’annexe A). On en déduit le flux réel de la puissance moyenne transportée par
l’onde
| (voir l’annexe A). On en déduit le flux réel de la puissance moyenne transportée par
l’onde
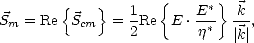 | (4.6) |
soit
 | (4.7) |
Le flux de puissance transportée par une onde EM est donc proportionnel à |E2|. Lorsque le signal
n’est plus une onde monochromatique mais un bruit thermique filtré dans une bande de pulsations de
largeur 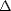
 , les paramètres de Stokes sont définis par ([104])
, les paramètres de Stokes sont définis par ([104])
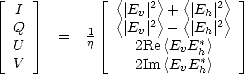
où 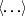 désigne une moyenne d’ensemble (les variations temporelles du champ
désigne une moyenne d’ensemble (les variations temporelles du champ 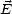 dans la bande de
pulsations
dans la bande de
pulsations 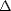
 sont statistiques et non plus harmoniques comme pour une onde monochromatique) et
sont statistiques et non plus harmoniques comme pour une onde monochromatique) et 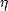 est l’impédance (réelle) de l’air.
est l’impédance (réelle) de l’air.
Les mesures effectuées par un radiomètre polarimétrique permettant de déterminer des températures de brillance sur deux polarisations orthogonales entre elles, on va modifier les paramètres de Stokes précédemment définis pour se ramener à ces quantités. On va donc premièrement définir des paramètres de Stokes modifiés Iv et Ih ([11, 89]), qui donnent respectivement la puissance radiative en V- et H-pol. On a ainsi le vecteur de Stokes modifié
avec Iv + Ih = I et Iv -Ih = Q. Deuxièmement, on va relier la température de brillance d’une source à sa puissance radiative, c’est à dire à Iv,Ih,U et V .
On définit la température de brillance en polarisation 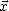 (Tbx) d’une source ayant une brillance
spectrale (i.e. émettant une puissance par unité de surface, d’angle solide et de fréquence) B
(Tbx) d’une source ayant une brillance
spectrale (i.e. émettant une puissance par unité de surface, d’angle solide et de fréquence) B ,x en
polarisation x comme la température physique du corps noir qui aurrait une brillance spectrale
(Bx cn /
,x en
polarisation x comme la température physique du corps noir qui aurrait une brillance spectrale
(Bx cn /
 ) en polarisation x identique à B
) en polarisation x identique à B ,x. La puissance émise par un corps noir (Bcn) en fonction de
sa température est donnée en (2.13). Comme l’émission d’un corps noir n’est pas polarisée, seule la moitié
de cette puissance émise l’est en polarisation x, d’où
,x. La puissance émise par un corps noir (Bcn) en fonction de
sa température est donnée en (2.13). Comme l’émission d’un corps noir n’est pas polarisée, seule la moitié
de cette puissance émise l’est en polarisation x, d’où

On en déduit
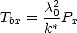 | (4.10) |
et
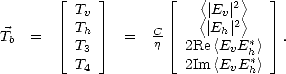
où
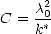 | (4.11) |
est la constante qui permet de passer d’une brillance spectrale à une Tb, k* = 1.3805 × 10-23JK-1 est
la constante de Boltzmann et 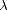 0 est la longueur d’onde du radiomètre. On définit de plus T1 = Tv + Th
et T2 = Tv - Th qui sont les équivalents en température de brillance des premier et second paramètres de
Stokes I et Q.
0 est la longueur d’onde du radiomètre. On définit de plus T1 = Tv + Th
et T2 = Tv - Th qui sont les équivalents en température de brillance des premier et second paramètres de
Stokes I et Q.
On peut, comme dans la section 2.3, exprimer la 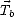 en terme d’émissivité
en terme d’émissivité 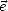 , et par conséquent en
terme de reflectivité
, et par conséquent en
terme de reflectivité 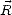 comme
comme
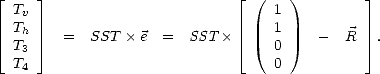
Les sections suivantes de ce chapitre sont consacrées au problème de la modélisation de l’émissivité, et
donc de la réflectivité 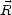 , de la surface océanique. Par la suite, je parlerai de Tb et de R respectivement
pour les éléments de
, de la surface océanique. Par la suite, je parlerai de Tb et de R respectivement
pour les éléments de 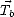 et de
et de 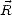 , c’est à dire respectivement pour Tv,Th,T3 ou T4 et Rv,Rh,R3 ou
R4 .
, c’est à dire respectivement pour Tv,Th,T3 ou T4 et Rv,Rh,R3 ou
R4 .