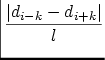A.2 Segmentation des traits

L'opération de segmentation d'un trait consiste à détecter les différents segments géométriques que représente un trait à main levée (voir section 4.4.3). La figure A.3 présente deux exemples de traits et leurs décompositions, les deux cas que l'on peut rencontrer lors d'un dessin à main levée: un trait représente un segment (voir figure A.3(a)) ou un trait représente plusieurs segments (voir figure A.3(b)).

Figure A.3: Segmentation de traits. Cette figure représente des traits dessinés (en noir) et les segments qu'ils représentent (en rouge).

L'expérience que nous avons du dessin d'architecte et l'étude que nous avons menée ont montrées que le premier cas est le plus fréquent, un trait continu représente souvent un seul segment. Dès lors, l'opération de segmentation est on ne peut plus simple: le segment correspondant au trait est composé par les deux points extrêmes de celui-ci (A et B dans la figure A.3(a)). Mais, dans notre paradigme de dessin à main levée sans contraintes, nous ne pouvons pas écarter le second cas que l'on rencontre tout de même plus ou moins fréquemment chez les dessinateurs (selon leur style ou leurs habitudes).
Dans ce cas général, le principe de la segmentation est de détecter, parmi les points capturés lors du tracé, ceux qui vont devenir les extrémités des segments (A, B, C et D dans la figure A.3(b)). Ces points sont appelés points critiques ou coins. Comme nous l'avons déjà évoqué dans ce mémoire, de nombreuses méthodes ont été proposées pour déterminer ces points dans les domaines de l'analyse d'images ou de l'interprétation temps réel. Nous ne détaillerons donc que celle que nous avons employée, combinant les données de courbure du trait et de vitesse de dessin en chaque point pour déterminer cette segmentation trait par trait.

A.2.1 Retour sur la méthode

Car en effet, beaucoup de travaux ont montré que le trait présente en ses points caractéristiques une courbure plus importante que les autres. C'est sur le calcul et l'analyse de cette donnée que sont basées la plupart des méthodes de détection. Toutefois, des variations trop minimes et lisses du rayon de courbure, ou des changements de direction trop fréquents peuvent entraîner la détection de «faux-positifs» ou l'omission de points. C'est pourquoi, dans une optique de détection temps réel où les information temporelle sont disponibles, Tevfik SEZGIN a proposé de combiner cette information de courbure avec la vitesse de dessin. À partir des résultats proposés dans [Lacquaniti et al.1983] et de mesures de la diminution de la vitesse de dessin au voisinage des points critiques, il a proposé dans [Sezgin et al.2001] une méthode hybride que nous avons reproduite pour la segmentation des traits dans SVALABARD.

Nous en donnerons ici les grandes lignes. Pour des justifications plus approfondies et des résultats plus précis de cette méthode, nous renvoyons le lecteur aux publications dont elle est tirée [Sezgin et al.2001,Sezgin2001]. Le principe général est de calculer, pour chaque point enregistré du trait, une «mesure de certitude» qui va représenter son aptitude à être un point critique du trait. Ensuite, il faut constituer un ensemble de solutions hybrides et choisir la meilleure d'entre elles.

A.2.1.1 Mesures de la certitude des points

Courbure.La première mesure est exprimée par la grandeur mesurée de la courbure au voisinage de chaque point p_i:

Formule A..1   Calcul de la mesure de courbure au voisinage d'un point.

$${\frac{{\vert d_{i-k}-d_{i+k}\vert}}{{l}}}$$

où l est la longueur de la courbe entre les points p_i-k et p_i+k, k est un entier qui définit la taille du voisinage considéré autour du point. Les valeurs d_i représentent la direction de la courbe au point p_i (l'angle formé par la tangente au trait au point donné avec l'axe des x).

Le calcul de la tangente soulève des problèmes de précision, résolus dans la méthode originale par l'utilisation d'une approximation numérique discrète: l'ODR (pour Orthogonal Distance Regression). Dans notre implémentation, nous avons utilisé un simple filtrage moyen des points qui assure une distance minimale entre deux points consécutifs pour un calcul simple par la formule: d = arctan(Δx, Δy)² (Δx et Δy représentent le changement de position relatif entre deux points). Bien que moins précis que la méthode originale, les résultats sont tout de même satisfaisants ^A.2. Enfin, cette mesure est normalisée pour obtenir des valeurs dans l'intervalle [0, 1] pour chaque point.

Vitesse.La seconde mesure correspond à une mesure du ralentissement du stylet en chaque point p_i, exprimée par:

Formule A..2   Calcul du ralentissement en un point.

1 - $${\frac{{v_i}}{{v_{max}}}}$$

où v_i est la vitesse instantanée entre les points p_i-1 et p_i, et v_max est la vitesse instantanée maximale atteinte lors du dessin du trait ^A.3.

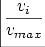
Cette mesure donne aussi des valeurs comprises dans l'intervalle [0, 1].

A.2.1.2 Ensemble de solutions hybrides

Ces premiers calculs donnent donc deux ensembles de points F_c et F_s, obtenus et triés par ordre décroissant à partir des données respectives de courbure et de vitesse. Une première solution hybride H₀ est alors construite par intersection de F_c et de F_s (le premier et le dernier point du trait, ainsi que les points de même ordre dans F_c et dans F_s).
Ensuite, deux nouvelles possibilités sont construites à partir de la solution précédente en lui ajoutant comme nouveau point caractéristique:

1. Le meilleur point candidat des données de vitesse. On obtient H'_i = H_i∪{p_s}.
2. Le meilleur point candidat des données de courbure. On obtient H''_i = H_i∪{p_c}.

À chacune de ces solutions est associée une mesure de pertinence, basée sur un calcul d'erreur aux moindres carrés: la somme moyenne des carrés des distances de chaque point du trait S à la solution.

Formule A..3   Calcul de l'erreur pour une solution.

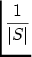
ε_i = 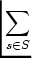$${\frac{{1}}{{\vert S\vert}}}$$$$\sum_{{s\in S}}^{}$$ODSQ(s, H_i)^A.4

Ainsi, des deux solution possibles (vitesse ou courbure), celle de plus faible erreur (la plus proche du trait original) est conservée et devient H_i+1. Les itérations continuent alors à partir de cette solution jusqu'à ce que tous les points candidats aient été utilisés afin de construire un ensemble de solutions hybrides.

A.2.1.3 Choix de la solution

Dès lors, le choix de la segmentation à conserver parmi l'ensemble construit nécessite d'établir un compromis entre l'augmentation du nombre de points et la diminution de l'erreur. La solution retenue et justifiée par l'auteur de cette méthode est de conserver comme unique solution celle dont l'erreur est en dessous d'un seuil fixé, avec le moins de points possibles. Dans notre implémentation, nous avons choisi de rendre ce seuil d'erreur paramétrable afin de pouvoir simplement et interactivement ajuster la précision de l'algorithme.

A.2.2 Algorithme

L'algorithme simplifié^A.5 A.1 donne une vue plus synthétique de ce traitement et de ses étapes.