Depuis le début de l'histoire de la radiométrie micro-onde, l'observation de la surface de la terre bénéficie des avancées technologiques dans l'observation de la voûte céleste. Ainsi, les premiers instruments ont été développés dans les années 30 et 40 par la communauté des astrophysiciens, les premières expériences de télédétection de la surface terrestre n'ayant lieu qu'à la fin des années 50 Ulaby. Depuis la fin des années 60, de nombreux satellites ont embarqué des radiomètres fonctionnant à diverses fréquences au sein du domaine micro-onde, fournissant ainsi des informations sur l'état de l'atmosphère (contenu en vapeur d'eau, en eau liquide, profils de températures, précipitation) et de la surface (SST, classification de la glace, de la couverture neigeuse, vitesse et direction du vent au dessus des océans...).
Le schéma 1.5 décrit les éléments principaux composant un radiomètre à puissance totale, qui est un dispositif à antenne réelle, par opposition aux interféromètres imageurs qui, on le verra par la suite, synthétisent une antenne. Tous les composants situés après l'antenne forment le récepteur. A eux deux, l'antenne et le récepteur vont définir deux caractéristiques importantes dans la télédétection par un radiomètre : la résolution spatiale et la sensibilité radiométrique. Les descriptions et les notions abordées par la suite seront utilisées dans les parties suivantes de ce document.
Résolution angulaire (
![]() [Rad])/spatiale (
[Rad])/spatiale (![]() x [
x [
![]() ]) et Sensibilité
radiométrique (
]) et Sensibilité
radiométrique (![]() [K]) pour un radiomètre à puissance totale
- la résolution
angulaire/spatiale, indique la taille du plus petit détail que l'instrument peut
distinguer dans la scène observée. La température de
brillance mesurée à un instant donné est
donc la température moyenne dans une zone dont la taille
est définie par
[K]) pour un radiomètre à puissance totale
- la résolution
angulaire/spatiale, indique la taille du plus petit détail que l'instrument peut
distinguer dans la scène observée. La température de
brillance mesurée à un instant donné est
donc la température moyenne dans une zone dont la taille
est définie par
![]() ou
ou ![]() x. La résolution spatiale
dépend fortement du diamètre D de l'antenne, de la
longueur d'onde
x. La résolution spatiale
dépend fortement du diamètre D de l'antenne, de la
longueur d'onde ![]() , ainsi que de l'altitude H de l'instrument :
, ainsi que de l'altitude H de l'instrument :
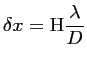 |
(1.9) |
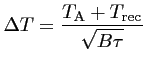 |
(1.10) |
L'antenne est l'élément qui fait le lien entre une onde électromagnétique se propageant librement (liée à la température de brillance mesurée) et un courant électrique oscillant se propageant au sein d'une ligne de transmission.
Avant tout, il faut bien comprendre que la température
![]() , appelée température d'antenne et qui caractérise
le champ électromagnétique arrivant sur l'antenne, n'est pas strictement
égale à la température
, appelée température d'antenne et qui caractérise
le champ électromagnétique arrivant sur l'antenne, n'est pas strictement
égale à la température
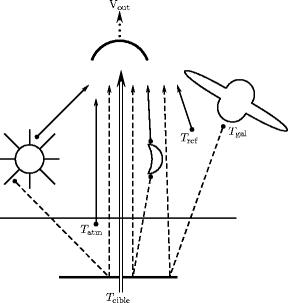
![]() de la scène observée. D'autres sources,
directes ou indirectes (voir Fig. 1.1), absolument
non négligeables, vont venir s'ajouter à celle-ci : citons le
soleil, la lune, la galaxie, le rayonnement cosmique fossile et enfin l'atmosphère.
Chacune de ses sources peuvent émettre dans la bande L mais aussi se refléter
sur la surface observée Aller.
de la scène observée. D'autres sources,
directes ou indirectes (voir Fig. 1.1), absolument
non négligeables, vont venir s'ajouter à celle-ci : citons le
soleil, la lune, la galaxie, le rayonnement cosmique fossile et enfin l'atmosphère.
Chacune de ses sources peuvent émettre dans la bande L mais aussi se refléter
sur la surface observée Aller.
De plus, le signal reçu est plus ou moins atténué suivant sa direction d'incidence : on dit que l'antenne n'est pas isotrope.
diagramme de rayonnement
![]() Le diagramme de rayonnement
(ou diagramme d'antenne) la capacité d'une antenne à
concentrer les ondes radio dans une direction (
Le diagramme de rayonnement
(ou diagramme d'antenne) la capacité d'une antenne à
concentrer les ondes radio dans une direction (
![]() )
donnée, où
)
donnée, où ![]() est l'angle d'incidence et
est l'angle d'incidence et ![]() , l'azimut.
, l'azimut.
La température d'antenne est alors définie comme suit :
température d'antenne [K]La température d'antenne est
la distribution de température de brillance ![]() arrivant sur
l'antenne (contribution de scène observée et contributions
secondaires) pondérée par le gain d'antenne et normalisée
par la somme du gain dans tout l'espace observé :
arrivant sur
l'antenne (contribution de scène observée et contributions
secondaires) pondérée par le gain d'antenne et normalisée
par la somme du gain dans tout l'espace observé :
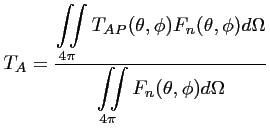 |
(1.11) |
L'efficacité ![]() d'une antenne est reliée la proportion
du signal capté par le lobe principal. Pour une antenne
(hypothétique) isotrope :
d'une antenne est reliée la proportion
du signal capté par le lobe principal. Pour une antenne
(hypothétique) isotrope :
| (1.12) | |||
| (1.13) |
Pour une antenne réelle, l'efficacité est inférieure à 1.
La puissance véritablement transmise par une antenne
de température physique
![]() est alors :
est alors :
| (1.14) | |||
| (1.15) |
RÉSOLUTION ANGULAIRE/SPATIALE
Comme on peut le voir sur la figure 1.5, une propriété
importante d'une antenne est de posséder un lobe principale, une région
de l'espace dans laquelle la majeure partie du signal est reçue. La largeur
à mi-hauteur (ou à -3dB) du lobe principal, notée
![]() , est sa largeur mesurée lorsque son intensité
vaut la moitié de son intensité maximale : plus
, est sa largeur mesurée lorsque son intensité
vaut la moitié de son intensité maximale : plus
![]() est petit, plus l'antenne est dite directive c.-à-d. plus
elle sera capable de discerner de petits détails.
est petit, plus l'antenne est dite directive c.-à-d. plus
elle sera capable de discerner de petits détails.
![]() est directement lié aux dimensions de l'antenne
(son diamètre
est directement lié aux dimensions de l'antenne
(son diamètre ![]() pour une antenne circulaire) et à la longueur d'onde d'observation.
La résolution angulaire d'un radiomètre est donc :
pour une antenne circulaire) et à la longueur d'onde d'observation.
La résolution angulaire d'un radiomètre est donc :
![$\displaystyle \delta \theta = \beta_{1/2}\approx \frac{\displaystyle \lambda}{D}~[\textrm{radians}]$](img83.gif) |
(1.16) |
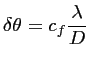 |
(1.17) |

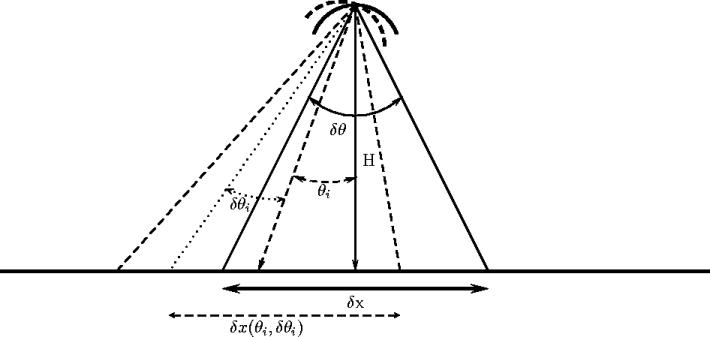
Une bonne approximation de la résolution spatiale (![]() x) d'un radiomètre situé à une altitude H à
la verticale de la scène observée (nadir pour l'instrument, zénith
pour la scène) consiste à calculer l'étalement du lobe principal
à l'intersection de la surface (la terre est supposée plate, voir
Fig. 1.3):
x) d'un radiomètre situé à une altitude H à
la verticale de la scène observée (nadir pour l'instrument, zénith
pour la scène) consiste à calculer l'étalement du lobe principal
à l'intersection de la surface (la terre est supposée plate, voir
Fig. 1.3):
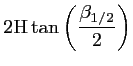 |
(1.18) | ||
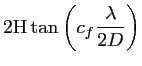 |
(1.19) |
En bande L, la longueur d'onde est de l'ordre de la dizaine de centimètres alors que les paraboles ont des diamètres de l'ordre du mètre. Par conséquent, une bonne approximation de la relation (3.6) est :
A diamètre et altitude fixés, la résolution spatiale est améliorée si la longueur d'onde est diminuée : on retrouve là un principe général de la mesure à distance qui dit que la taille du plus petit détail visible par un instrument est proportionnelle à la longueur d'onde d'observation. A longueur d'onde et altitude fixées, la résolution spatiale est améliorée si le diamètre de l'antenne est augmenté et donc si la largeur du lobe principal diminue : si l'on était amené à décrire un objet les yeux fermés, à distance, à l'aide d'une baguette, notre analyse serait d'autant plus précise que le diamètre de la baguette serait réduit. Il en va de même pour la largeur à mi-hauteur du lobe principal de l'antenne, qui représente la taille de la baguette du radiomètre.
Pour finir, si l'antenne est inclinée d'un angle ![]() (voir Fig. 1.3), et en considérant
une cible située à
(voir Fig. 1.3), et en considérant
une cible située à
![]() , la relation (1.20)
devient :
, la relation (1.20)
devient :
La figure 1.5 montre un récepteur dit super-hétérodyne.
Son but est de fournir en sortie un courant
![]() mesurable et proportionnel à la puissance
reçue par l'antenne. Pour cela, la puissance à la sortie de l'antenne
est amplifiée et la fréquence du signal translatée vers des domaines
plus facilement manipulables par l'électronique. Or, ces opérations
vont ajouter un bruit à la température d'antenne, dégradant la
précision radiométrique.
mesurable et proportionnel à la puissance
reçue par l'antenne. Pour cela, la puissance à la sortie de l'antenne
est amplifiée et la fréquence du signal translatée vers des domaines
plus facilement manipulables par l'électronique. Or, ces opérations
vont ajouter un bruit à la température d'antenne, dégradant la
précision radiométrique.
Ainsi, la tension
![]() mesuré à la fin de la chaîne de réception n'est pas
proportionnelle à la puissance
mesuré à la fin de la chaîne de réception n'est pas
proportionnelle à la puissance
![]() délivrée
par l'antenne mais à la puissance
délivrée
par l'antenne mais à la puissance
![]() du système qui
fait intervenir la température de bruit
du système qui
fait intervenir la température de bruit
![]() générée par
l'ensemble des systèmes de traitement.
générée par
l'ensemble des systèmes de traitement.
| (1.22) | |||
| (1.23) |
Le gain ![]() d'un élément de la chaîne de réception caractérise
le facteur d'amplification de la puissance d'entrée
d'un élément de la chaîne de réception caractérise
le facteur d'amplification de la puissance d'entrée
![]() . Il
s'exprime généralement en décibels :
. Il
s'exprime généralement en décibels :
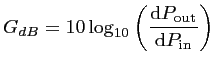 |
(1.24) |
Si le bruit en entrée est caractérisé par une température
![]() et que la propre température de bruit de l'élément
considéré est
et que la propre température de bruit de l'élément
considéré est
![]() , alors la puissance du bruit en sortie
, alors la puissance du bruit en sortie
![]() sera :
sera :
| (1.25) |
La figure de bruit de ce même élément exprime la dégradation du rapport signal sur bruit entre l'entrée et la sortie :
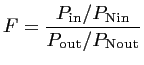 |
(1.26) |
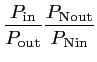 |
(1.27) | ||
| (1.28) | |||
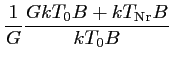 |
(1.29) | ||
| (1.30) | |||
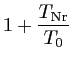 |
(1.31) |
La température de bruit d'un élément de la chaîne de réception est donc proportionnelle à la température de bruit en entrée :
Le gain d'un récepteur composé de N éléments est simplement le produit des gains de chacun de ces éléments :
| (1.33) |
La contribution de la température de bruit d'un composant à la température de
bruit du récepteur
![]() est pondérée par le gain des
composants qui le précède :
est pondérée par le gain des
composants qui le précède :
Le facteur de perte ![]() , l'inverse du gain
, l'inverse du gain ![]() caractérise la fuite de
puissance qui intervient tout au long de la chaîne de
réception :
caractérise la fuite de
puissance qui intervient tout au long de la chaîne de
réception :
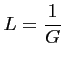 |
(1.35) |
La température de bruit véritablement induite par un
récepteur de température physique
![]() est alors :
est alors :
| (1.36) |
Les différents composants d'un récepteur de type super-hétérodyne sont décrits ci-dessous.
. L'amplificateur Radio-Fréquence (RF)
Sa fonction est d'amplifier le signal puisque la
puissance à la sortie de l'antenne est de l'ordre de
![]() W Ulaby Salter. Le gain typique d'un tel amplificateur est de
l'ordre
W Ulaby Salter. Le gain typique d'un tel amplificateur est de
l'ordre
![]() dB. Comme il est rappelé ci-dessus,
cette étape est critique pour la sensibilité radiométrique.
dB. Comme il est rappelé ci-dessus,
cette étape est critique pour la sensibilité radiométrique.
. Le filtre passe-bande
Bien entendu, le signal RF reçu et transmis par l'antenne
comporte une large gamme de fréquences. Or, en bande L, seule une
étroite zone est protégée des émissions artificielles comme
les ondes de télécommunications (téléphones portables,
relais...) ou encore les radars des aéroports. Le filtre
passe-bande à pour objectif de sélectionner le signal à
l'intérieur de cette zone. Toutefois, ce n'est pas ce filtre
qui définit la bande passante de l'ensemble du récepteur,
mais celui situé après l'amplificateur à fréquence
intermédiaire. La bande passante est ici un peu plus large
que la bande passante nominale du récepteur.
. Le mélangeur
Le signal RF à l'entrée du mélangeur est centré sur la
fréquence centrale d'observation
![]() (
(![]() 1.41 GHz
en bande L). L'objectif du mélangeur est d'abaisser
fortement la fréquence de l'onde porteuse du signal RF pour
l'amener à une fréquence intermédiaire
1.41 GHz
en bande L). L'objectif du mélangeur est d'abaisser
fortement la fréquence de l'onde porteuse du signal RF pour
l'amener à une fréquence intermédiaire
![]() de l'ordre de 5 à
30 MHz. Ainsi, le signal sera plus facilement traitable par
l'électronique et, en cas de fuite de signal, on évitera un
retour vers l'antenne, une boucle positive et une
oscillation de l'ensemble du récepteur Salter.
de l'ordre de 5 à
30 MHz. Ainsi, le signal sera plus facilement traitable par
l'électronique et, en cas de fuite de signal, on évitera un
retour vers l'antenne, une boucle positive et une
oscillation de l'ensemble du récepteur Salter.
Le mélange consiste à multiplier le signal RF par une sinusoïde de fréquence
![]() . La fréquence
intermédiaire
. La fréquence
intermédiaire
![]() est alors définie par :
est alors définie par :
| (1.37) |
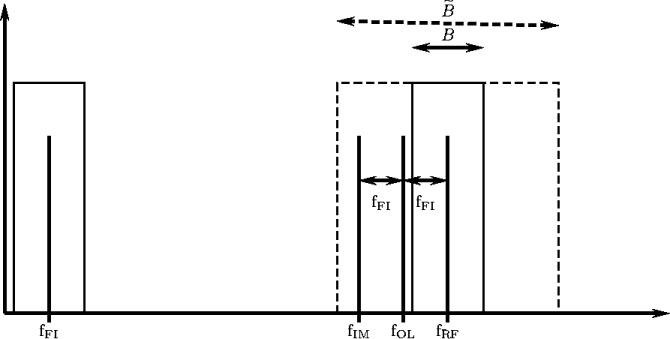
. Le filtre passe-bande
C'est la bande passante de ce filtre qui définira la bande
passante du récepteur.
. Le
détecteur quadratique
Le but est d'obtenir en sortie un courant dont la tension
sera proportionnelle au carré du courant en entrée et donc
proportionnelle à la puissance
![]() délivrée par l'ensemble de la
chaîne d'acquisition. En entrée, le signal est alternatif,
en sortie, il est continu. Un détecteur typique est une
simple diode.
délivrée par l'ensemble de la
chaîne d'acquisition. En entrée, le signal est alternatif,
en sortie, il est continu. Un détecteur typique est une
simple diode.
. Le filtre
passe-bas ou Intégrateur
A l'entrée de ce composant, le courant continu comporte
encore de fortes fluctuations hautes-fréquences qui, si
elles n'étaient pas éliminées, réduiraient fortement la
sensibilité radiométrique de l'instrument. Le lissage du
signal est réalisée par un filtre passe-bas caractérisé par
un temps de lissage, ou temps d'intégration ![]() . Ce
filtre passe-bas est donc aussi appelé intégrateur puisque
le courant en sortie est une moyenne du courant d'entrée sur
un temps
. Ce
filtre passe-bas est donc aussi appelé intégrateur puisque
le courant en sortie est une moyenne du courant d'entrée sur
un temps ![]() . Le plus simple des intégrateurs est une
circuit RC avec
. Le plus simple des intégrateurs est une
circuit RC avec ![]() RC.
RC.

SENSIBILITÉ RADIOMÉTRIQUE
L'équation du radiomètre donne la sensibilité
radiométrique ![]() en fonction de la température système
en fonction de la température système
![]() , de la largeur de bande
, de la largeur de bande ![]() du récepteur et du temps
d'intégration
du récepteur et du temps
d'intégration ![]() :
:
Cette sensibilité radiométrique ne tient pas compte des
variations possibles du gain ![]() du récepteur. Ce
dernier peut être défini comme le coefficient de
proportionnalité entre
du récepteur. Ce
dernier peut être défini comme le coefficient de
proportionnalité entre
![]() et
et
![]() :
:
L'objet même de l'étalonnage est de quantifier ![]() . Si l'on suppose que la relation (1.40)
est linéaire, une mesure du courant de sortie pour deux températures
de bruit, l'une froide l'autre chaude , directement injectées à
la sortie de l'antenne, permet de retrouver
. Si l'on suppose que la relation (1.40)
est linéaire, une mesure du courant de sortie pour deux températures
de bruit, l'une froide l'autre chaude , directement injectées à
la sortie de l'antenne, permet de retrouver ![]() . Cependant, cela ne peut prendre en compte les variations
rapides du gain du récepteur, entre chaque procédure d'étalonnage.
La sensibilité radiométrique
. Cependant, cela ne peut prendre en compte les variations
rapides du gain du récepteur, entre chaque procédure d'étalonnage.
La sensibilité radiométrique
![]() de la relation (
de la relation (![]() ), dont l'origine est la
température de bruit du récepteur, est distinguée de la sensibilité
), dont l'origine est la
température de bruit du récepteur, est distinguée de la sensibilité
![]() , dont l'origine est la variation du gain
, dont l'origine est la variation du gain ![]() :
:
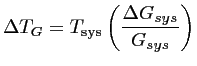 |
(1.41) |
![$\displaystyle \left[ (\Delta T_N)^2 + (\Delta T_G)^2 \right]^{1/2}$](img154.gif) |
(1.42) | ||
![$\displaystyle T_{\textrm{sys}}\left[ \frac{\displaystyle 1}{B\tau} + \left( \frac{\displaystyle \Delta G_{sys}}{G_{sys}} \right)^2 \right]^{1/2}$](img155.gif) |
(1.43) |
Etant donnée la relation (1.20), pour obtenir une
résolution spatiale, au nadir, de 50 km à 750 km d'altitude,
pour une longueur d'onde de 20 cm et un coefficient ![]() , un radiomètre doit posséder une antenne d'un
diamètre d'un diamètre de :
, un radiomètre doit posséder une antenne d'un
diamètre d'un diamètre de :
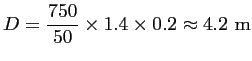 |
(1.44) |
D'après l'équation (1.34),
![]() dépend largement de la température de bruit
de l'amplificateur RF. La figure de bruit de ce dernier étant de l'ordre
de 2.3 dB et, d'après (1.32), sa température
de bruit est :
dépend largement de la température de bruit
de l'amplificateur RF. La figure de bruit de ce dernier étant de l'ordre
de 2.3 dB et, d'après (1.32), sa température
de bruit est :
| (1.45) |
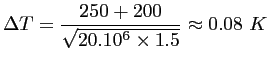 |
(1.46) |
Cependant, pour ce qui est de la résolution spatiale et de la propriété de mesure multi-angulaire, une autre technique de mesure doit être envisagée. Le chapitre suivant expose les principes fondamentaux de la technique de synthèse d'ouverture.
Biographie(s)
