Next: 2.3 Fondements physiques :
Up: 2. Principes fondamentaux de
Previous: 2.1 Présentation générale des
Contenu
Prenons l'exemple d'un accord de La mineur joué par
un piano et obtenu par la pression simultanée sur quatre touches
: La (grave), Mi, Do et de nouveau La (aigu). Le son entendu correspond a une
vibration des cordes transmise à l'air puis à notre tympan :
il se propage comme une onde, une variation périodique de
la pression de l'air. Près de notre oreille vont donc se
succéder plusieurs fois par seconde des zones de pressions,
alternativement fortes et faibles. La hauteur du son est
déterminé par la distance entre deux extrema (la longueur
d'onde [m]) ou encore, ce qui est équivalent, par le nombre
d'oscillations par seconde (la fréquence temporelle exprimée
en HERTZ) : plus la longueur d'onde est grande,
plus la fréquence est petite et plus le son est grave et
inversement, plus la longueur d'onde est petite, plus la
fréquence est grande et plus le son est aigu. Ainsi, les
quatre notes formant l'accord de La mineur ont les fréquences
suivantes : La (grave) = 220 Hz (220 battements par
seconde), Mi = 329.6 Hz, La (aigu) = 440 Hz, Do = 523.3 Hz.
La figure 2.3 illustre la superposition de ces notes :
en haut, un accord de La mineur sur une portée ouverte par une clé
de sol, au centre les variations de pressions au cours du temps pour cet accord
et en bas, les quatre notes, les quatre vibrations élémentaires. Un
musicien expérimenté peut discerner les notes composant un accord
à son écoute mais cette distinction est plus difficile pour un néophyte.
JOSEPH FOURIER a été le premier à
présenter une méthode permettant de décomposer tout signal en
une superposition de signaux périodiques de fréquence donnée
Fourier1 Fourier2. L'objet de la transformée de Fourier est d'indiquer
quelles fréquences sont présentes dans ce signal et avec quelle importance
. Ainsi, la figure 2.3 montre aussi la transformée de
Fourier de l'onde sonore (appelée spectre de fréquence) engendrée
par un accord de La mineur : on y retrouve les quatre fréquences des notes
qui le composent, avec la même importance dans un cas idéal.
La transformée de FOURIER (notée
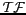 par la suite) peut aussi s'appliquer à
l'étude de signaux variant non pas en fonction du temps mais
en fonction d'une distance. Les fréquences ne sont alors plus
temporelles mais spatiales. En réalité, il est abusif de parler de la
transformée de FOURIER, puisque les relations changent
selon que le signal étudié est continu ou discret,
périodique ou non. Dans ce paragraphe, nous parcourrons les
différentes transformées de FOURIER pour aboutir à la transformée de
FOURIER discrète de signaux périodiques et discrets.
par la suite) peut aussi s'appliquer à
l'étude de signaux variant non pas en fonction du temps mais
en fonction d'une distance. Les fréquences ne sont alors plus
temporelles mais spatiales. En réalité, il est abusif de parler de la
transformée de FOURIER, puisque les relations changent
selon que le signal étudié est continu ou discret,
périodique ou non. Dans ce paragraphe, nous parcourrons les
différentes transformées de FOURIER pour aboutir à la transformée de
FOURIER discrète de signaux périodiques et discrets.
Les relations entre une image 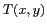 définie continûment dans tout
l'espace et sa transformée de Fourier
définie continûment dans tout
l'espace et sa transformée de Fourier
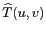 sont les suivantes :
sont les suivantes :
Figure 2.3: L'accord de La mineur vu comme la superposition
de ses quatre fondamentales : en haut, cet accord écrit sur une portée,
en dessous, les variations correspondantes de pression au cours du temps,
3
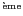 ligne, les variations de pression pour (de gauche à
droite) un La (grave), un Mi, un Do et un La (aigu). En bas, la transformée
de Fourier du signal fait apparaître les quatre fréquences qui le
composent.
ligne, les variations de pression pour (de gauche à
droite) un La (grave), un Mi, un Do et un La (aigu). En bas, la transformée
de Fourier du signal fait apparaître les quatre fréquences qui le
composent.
|
|
Rappelons quelques propriétés de la transformée de FOURIER continue d'un signal continu.
Egalité de PARSEVAL
L'énergie contenue dans l'image est conservée par la
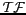 :
:
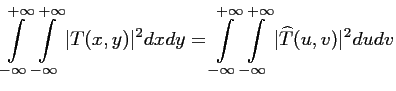 |
(2.8) |
Propriété de convolution de la
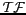 La
La
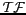 d'un produit de deux fonctions
d'un produit de deux fonctions
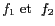 est égale à la
convolution de leur
est égale à la
convolution de leur
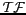 respective,
respective,
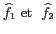 :
:
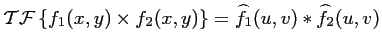 |
(2.9) |
Propriété de translation de la
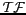 La translation d'une image se traduit par un déphasage de
son spectre :
La translation d'une image se traduit par un déphasage de
son spectre :
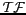 d'un peigne de DIRAC
La transformée de Fourier d'un peigne de DIRAC caractérisé
par un pas
d'un peigne de DIRAC
La transformée de Fourier d'un peigne de DIRAC caractérisé
par un pas 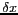 est un peigne de DIRAC caractérisé par
un pas
est un peigne de DIRAC caractérisé par
un pas
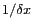 et dont l'amplitude est multipliée par
et dont l'amplitude est multipliée par
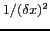 :
:
Dans la pratique, deux caractéristiques de l'acquisition numérique
d'une scène 2D vont venir modifier les propriétés de son
spectre : l'échantillonnage d'une image va conduire à une
périodisation de son spectre et la périodisation de cette
image va conduire à l'échantillonnage de son spectre.
Les seules quantités manipulables par un
ordinateur sont discrètes. Cet échantillonnage
![$ T[k,l]$](img220.gif) de pas
de pas 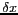 peut être vu comme la multiplication de la scène continue
peut être vu comme la multiplication de la scène continue
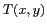 par un peigne de DIRAC 2D
par un peigne de DIRAC 2D
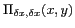 :
:
![$\displaystyle T[k,l] = T(k\delta x,l\delta x) = T(x,y) \Pi_{\delta x, \delta x}(x,y)$](img222.gif) |
(2.13) |
Ainsi, l'échantillonnage va conduire, dans le calcul de la
transformée de FOURIER, à une convolution des
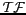 de l'image et du peigne de DIRAC et à une périodisation
de l'image et du peigne de DIRAC et à une périodisation
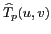 du spectre :
du spectre :
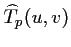 |
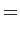 |
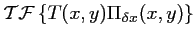 |
(2.14) |
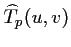 |
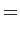 |
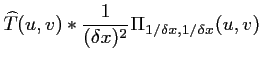 |
(2.15) |
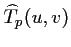 |
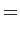 |
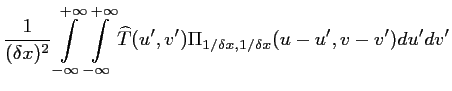 |
(2.16) |
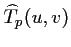 |
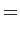 |
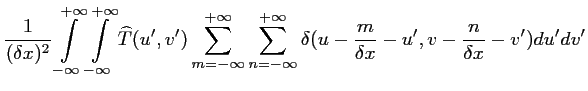 |
(2.17) |
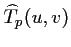 |
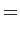 |
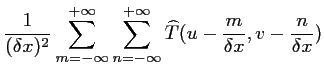 |
(2.18) |
où
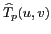 est une fonction
est une fonction
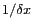 -périodique.
-périodique.
On peut alors se demander quelle doit être la finesse du pas 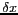 pour que l'échantillonnage d'une image continue se fasse
sans perte d'information. Le critère de Shannon-Nyquist L'échantillonnage
d'un signal continu, dont le spectre est borné par une fréquence maximale
pour que l'échantillonnage d'une image continue se fasse
sans perte d'information. Le critère de Shannon-Nyquist L'échantillonnage
d'un signal continu, dont le spectre est borné par une fréquence maximale
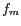 , se fait sans perte d'information si le pas d'échantillonnage
vérifie
, se fait sans perte d'information si le pas d'échantillonnage
vérifie
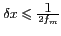 . Reprenons alors le
résultat (2.18). Il peut être vu comme une relation
entre la transformée de FOURIER
. Reprenons alors le
résultat (2.18). Il peut être vu comme une relation
entre la transformée de FOURIER
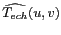 du signal échantillonné
du signal échantillonné
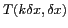 et la
et la
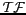
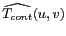 du signal continu
du signal continu 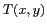 :
:
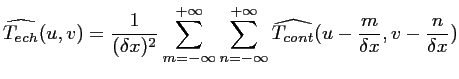 |
(2.19) |
Or, si le critère de SHANNON est respecté,
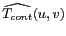 est nul pour
est nul pour
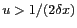 et
et
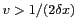 . On obtient donc une
relation entre la
. On obtient donc une
relation entre la
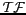 d'un signal échantillonné et
la
d'un signal échantillonné et
la
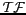 de ce même signal dans sa version continue :
de ce même signal dans sa version continue :
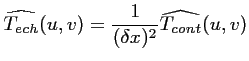 |
(2.20) |
Les relations entre un signal discret non périodique et sa
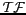 sont les suivantes :
sont les suivantes :
L'acquisition d'une image implique de limiter
ses dimensions : afin de pouvoir appliquer la
transformée de Fourier, on considérera une répétition de
cette image dans tout l'espace. Une telle périodisation de la scène implique la
discrétisation de son spectre.
Les relations entre un signal 2D discret périodique de
dimensions 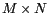 et sa
et sa
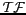 sont alors les suivantes :
sont alors les suivantes :
Ces relations définissent la transformée de FOURIER à
deux dimensions (
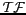 D). Le calcul de
D). Le calcul de
![$ \widehat {T}[m,n]$](img250.gif) à l'aide de la relation (2.24)
implique
à l'aide de la relation (2.24)
implique 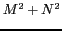 opérations. Des algorithmes ont été développés
afin de réduire de nombre d'opérations à
opérations. Des algorithmes ont été développés
afin de réduire de nombre d'opérations à
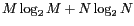 : on appelle ces méthodes des transformées
de FOURIER rapides ou FFT pour Fast FOURIER Transform.
: on appelle ces méthodes des transformées
de FOURIER rapides ou FFT pour Fast FOURIER Transform.
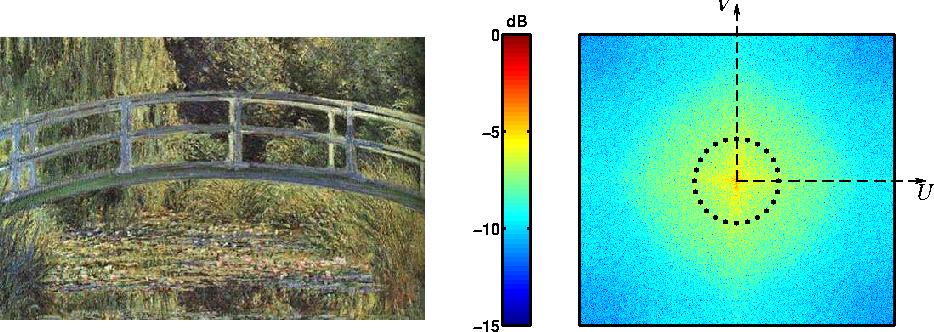
Un exemple illustre les relations précédentes : il s'agit d'un tableau
de CLAUDE MONNET, Le bassin aux nymphéas ,
peint en 1899 et représentant une scène souvent utilisée par Monnet,
celle du pont japonais enjambant un bassin couvert par des nénuphars. La
figure 2.4 montre à gauche un échantillonnage de
l'oeuvre originale, chacun des 500x333=166500 pixels qui la composent portant
une information sur la couleur.
La
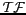 d'une image étant une quantité complexe,
le spectre présenté à droite sur la figure 2.4
est lié au spectre d'amplitude
d'une image étant une quantité complexe,
le spectre présenté à droite sur la figure 2.4
est lié au spectre d'amplitude
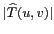 . Certaines caractéristiques de
l'image peuvent apparaître par une simple étude de sa transformée
de Fourier. Ainsi, la relation 2.23 montre que la valeur
de la
. Certaines caractéristiques de
l'image peuvent apparaître par une simple étude de sa transformée
de Fourier. Ainsi, la relation 2.23 montre que la valeur
de la
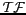 à la fréquence nulle
à la fréquence nulle 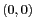 est la valeur moyenne de la quantité
est la valeur moyenne de la quantité 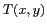 , dans le cas de notre image, sa couleur moyenne. L'essentiel
de l'énergie d'une image est contenue dans cette valeur, c'est pourquoi
l'écart entre la valeur d'une
, dans le cas de notre image, sa couleur moyenne. L'essentiel
de l'énergie d'une image est contenue dans cette valeur, c'est pourquoi
l'écart entre la valeur d'une
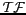 à la fréquence nulle et à une fréquence
non nulle, même faible, est grande. La figure 2.4
représente donc la transformée de Fourier en échelle logarithmique,
à la fréquence nulle et à une fréquence
non nulle, même faible, est grande. La figure 2.4
représente donc la transformée de Fourier en échelle logarithmique,
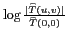 . En
reconstruisant une image à partir des seules fréquences contenues
à l'intérieur du cercle en pointillé de la figure 2.4,
on obtient une version basse fréquence dans laquelle apparaît une
information sur le contraste, sur les grandes échelles de l'oeuvre originale.
Au contraire, la version haute fréquence obtenue à partir des fréquences
extérieures cercle en pointillé donne une information sur les contours
et sur les détails.
. En
reconstruisant une image à partir des seules fréquences contenues
à l'intérieur du cercle en pointillé de la figure 2.4,
on obtient une version basse fréquence dans laquelle apparaît une
information sur le contraste, sur les grandes échelles de l'oeuvre originale.
Au contraire, la version haute fréquence obtenue à partir des fréquences
extérieures cercle en pointillé donne une information sur les contours
et sur les détails.
La reconstruction basse fréquence montrée sur la figure 2.5
est un exemple de signal à spectre borné, dit encore à bande
passante limitée : les composantes de Fourier de cette image sont nulles
pour les fréquences situées au delà du cercle pointillé.
La bande passante a ici la forme d'un disque dont le rayon est égal à
la fréquence de coupure. Il est alors intéressant de noter qu'une
image à bande passante possède une résolution (un niveau de détail)
plus faible que l'image originale.
Figure 2.4: A gauche, Le bassin aux nymphéas , de CLAUDE
MONNET (1899, Musée d'Orsay). A droite,
sa transformée de Fourier à deux dimensions.
Figure 2.5: A gauche, la composante basse fréquence
du bassin aux nymphéas , à droite, la composante haute fréquence.




Next: 2.3 Fondements physiques :
Up: 2. Principes fondamentaux de
Previous: 2.1 Présentation générale des
nous
2005-03-31
![]() par la suite) peut aussi s'appliquer à
l'étude de signaux variant non pas en fonction du temps mais
en fonction d'une distance. Les fréquences ne sont alors plus
temporelles mais spatiales. En réalité, il est abusif de parler de la
transformée de FOURIER, puisque les relations changent
selon que le signal étudié est continu ou discret,
périodique ou non. Dans ce paragraphe, nous parcourrons les
différentes transformées de FOURIER pour aboutir à la transformée de
FOURIER discrète de signaux périodiques et discrets.
par la suite) peut aussi s'appliquer à
l'étude de signaux variant non pas en fonction du temps mais
en fonction d'une distance. Les fréquences ne sont alors plus
temporelles mais spatiales. En réalité, il est abusif de parler de la
transformée de FOURIER, puisque les relations changent
selon que le signal étudié est continu ou discret,
périodique ou non. Dans ce paragraphe, nous parcourrons les
différentes transformées de FOURIER pour aboutir à la transformée de
FOURIER discrète de signaux périodiques et discrets.
![]() définie continûment dans tout
l'espace et sa transformée de Fourier
définie continûment dans tout
l'espace et sa transformée de Fourier
![]() sont les suivantes :
sont les suivantes :
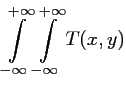 e
e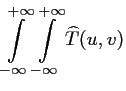 e
e![]() :
:
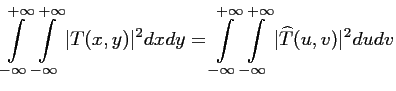
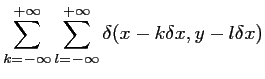
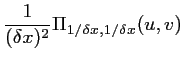
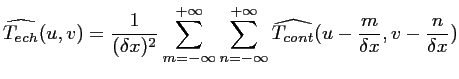
![]() d'une image étant une quantité complexe,
le spectre présenté à droite sur la figure 2.4
est lié au spectre d'amplitude
d'une image étant une quantité complexe,
le spectre présenté à droite sur la figure 2.4
est lié au spectre d'amplitude
![]() . Certaines caractéristiques de
l'image peuvent apparaître par une simple étude de sa transformée
de Fourier. Ainsi, la relation 2.23 montre que la valeur
de la
. Certaines caractéristiques de
l'image peuvent apparaître par une simple étude de sa transformée
de Fourier. Ainsi, la relation 2.23 montre que la valeur
de la
![]() à la fréquence nulle
à la fréquence nulle ![]() est la valeur moyenne de la quantité
est la valeur moyenne de la quantité ![]() , dans le cas de notre image, sa couleur moyenne. L'essentiel
de l'énergie d'une image est contenue dans cette valeur, c'est pourquoi
l'écart entre la valeur d'une
, dans le cas de notre image, sa couleur moyenne. L'essentiel
de l'énergie d'une image est contenue dans cette valeur, c'est pourquoi
l'écart entre la valeur d'une
![]() à la fréquence nulle et à une fréquence
non nulle, même faible, est grande. La figure 2.4
représente donc la transformée de Fourier en échelle logarithmique,
à la fréquence nulle et à une fréquence
non nulle, même faible, est grande. La figure 2.4
représente donc la transformée de Fourier en échelle logarithmique,
![]() . En
reconstruisant une image à partir des seules fréquences contenues
à l'intérieur du cercle en pointillé de la figure 2.4,
on obtient une version basse fréquence dans laquelle apparaît une
information sur le contraste, sur les grandes échelles de l'oeuvre originale.
Au contraire, la version haute fréquence obtenue à partir des fréquences
extérieures cercle en pointillé donne une information sur les contours
et sur les détails.
. En
reconstruisant une image à partir des seules fréquences contenues
à l'intérieur du cercle en pointillé de la figure 2.4,
on obtient une version basse fréquence dans laquelle apparaît une
information sur le contraste, sur les grandes échelles de l'oeuvre originale.
Au contraire, la version haute fréquence obtenue à partir des fréquences
extérieures cercle en pointillé donne une information sur les contours
et sur les détails.